逆向分析加解密之TwoFish算法
本文由本人首发于先知社区 https://xz.aliyun.com/t/5807
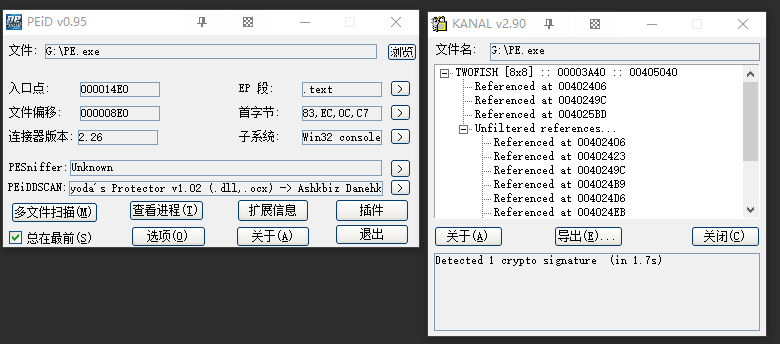
前几天某师傅给我发来一个逆向题，拿来分析发现竟是AES决赛算法之一的TwoFish算法，之前网上对此算法的逆向分析竟然一个都没有，对算法的介绍也只有寥寥数语，于是想准备在这里与大家分享对该算法的逆向分析以及CTF中此算法的变体。
算法流程
官方有一个68页的pdf，有兴趣可以看一下
http://www.schneier.com/twofish-analysis-shiho.pdf
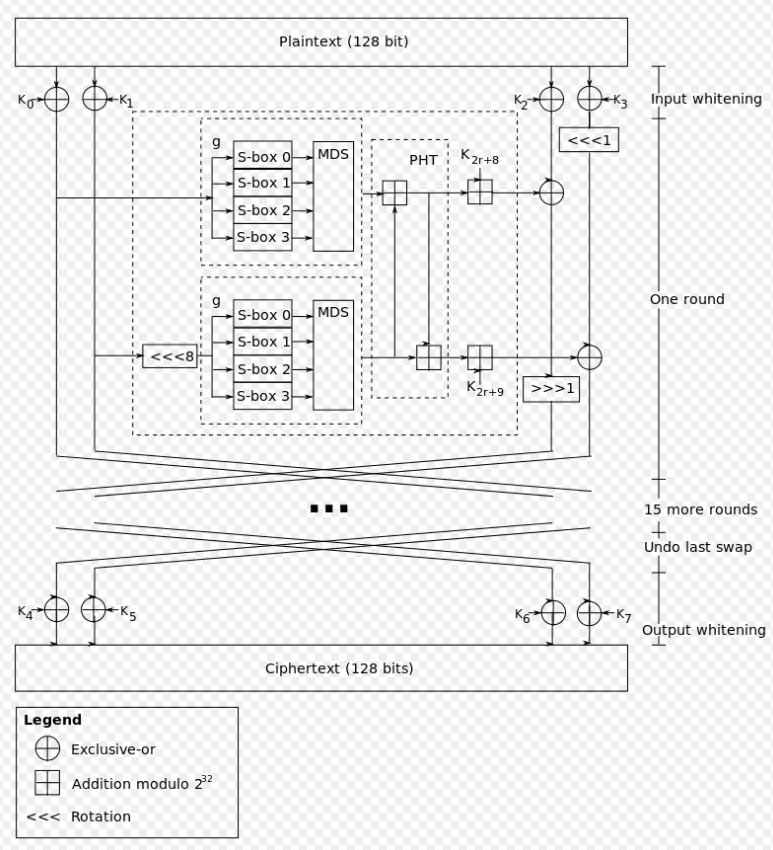
流程图
TwoFish的意思应该就是这样交叉运算的形状吧
算法分析
TwoFish加密需要明文(plain)和密钥(key)
总的来说进行一次加解密可分为三个环节
- Input whitening
- 16次循环
- Output whitening
Input whitening
- 拓展密钥
在Twofish 算法中，规定密钥的长度 N = 128, N = 192, N = 256三种。也就是说密钥的长度可以在128-bit ~ 256-bit之间变化。
我们需要产生40个与密钥相关的K(i)，这里的K(i)是根据密钥算出来的32-bit数据
除此以外，我们还需要4个与密钥相关的S-box，也就是s(i)()。
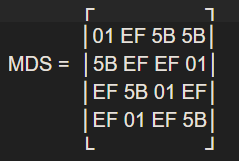
为计算K和S，定义MDS矩阵
且对于MDS 矩阵，有限域GF的定义如下：GF(2^8) ≡ GF(2)(x)/v(x)，其中v(x) = x^8 + x^6 + x^5 + x^3 + 1
此外还需要h函数
y(k,j) = x(j) j = 0, ... ,3
如果：k == 4
y(3,0) = q1[y(4,0)] xor l(3,0)
y(3,1) = q0[y(4,1)] xor l(3,1)
y(3,2) = q0[y(4,2)] xor l(3,2)
y(3,3) = q1[y(4,3)] xor l(3,3)
如果：k >= 3
y(2,0) = q1[y(3,0)] xor l(2,0)
y(2,1) = q1[y(3,1)] xor l(2,1)
y(2,2) = q0[y(3,2)] xor l(2,2)
y(2,3) = q0[y(3,3)] xor l(3,3)
对于所有情况：
y0 = q1[q0[q0[y(2,0)] xor l(1,0)] xor l(0,0)]
y1 = q0[q0[q1[y(2,1)] xor l(1,1)] xor l(0,1)]
y2 = q1[q1[q0[y(2,2)] xor l(1,2)] xor l(0,2)]
y3 = q0[q1[q1[y(2,3)] xor l(1,3)] xor l(0,3)]实现代码稍后来说
- 输入白化
因为加密前的plain text是128 bits，也就是16 bytes。假设这16 bytes分别是p0, … ,p15。将p0, … ,p15分为4组：P(i) = ∑p(4i+j)2^(8j)，其中i,j = 0, ... ,3
然后进行运算R(0,i) = P(i) xor K(i)，其中i = 0, ... ,3
16次运算
将以下公式循环16次
(F(r,0), F(r,1)) = F(R(r,0), R(r,1), r)
R(r+1,0) = ROR(R(r,2) xor F(r,0), 1)
R(r+1,1) = ROL(R(r,3), 1) xor F(r,1)
R(r+1,2) = R(r,0)
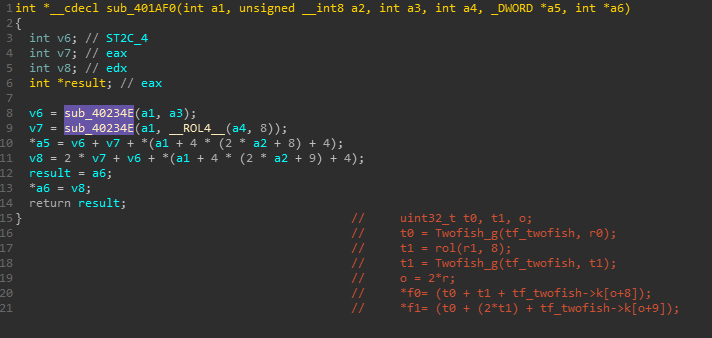
R(r+1,3) = R(r,1)其中，F函数为以下操作
t0 = g(r0)
t1 = rol(r1, 8)
t1 = g(t1)
o = 2*r
F0 = (T0 + T1 + K(2r+8)) mod 2^32
F1 = (T0 + 2T1 + K(2r+9)) mod 2^32其中g函数为核心函数
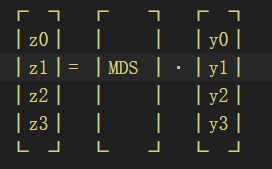
x(i) = [X/2^(8i)] mod 2^8 其中i = 0, ... ,3
y(i) = s(i)(x(i)) 其中i = 0, ... ,3
Z = ∑z(i)2^(8i)，其中i = 0, ... ,3输出白化
C(i) = R(16,(i+2) mod 4) xor K(i+4)，其中i = 0, ... ,3最后计算组成密文
c(i) = [C(i/4) / 2^(8(i mod 4))] mod 2^8，其中i = 0, ... ,15下面来逆向分析看一下实际实现吧
逆向分析
拿到题后PEID分析
分析到了TwoFish算法
IDA分析一下，进入主函数看到流程
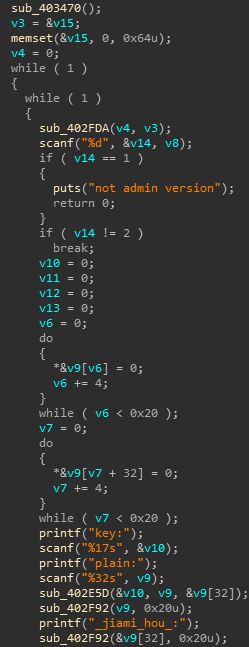
发现有五个选项，选项名字在sub_402FDA中
cpp
int sub_402FDA() |
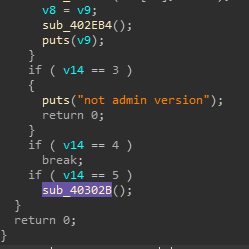
只有选项2和5可用，即加密和验证flag
进入验证函数sub_40302B查看
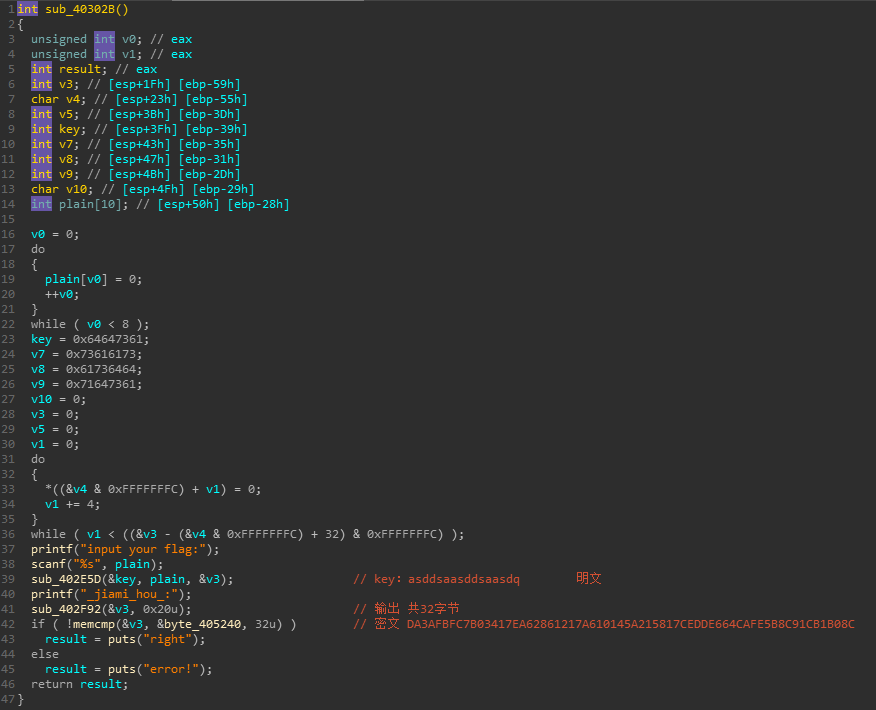
这里我已经注释出密文和key，因此我们只需要解密即可，但只用标准解密算法就可以吗？我们来验证一下
很明显加密函数为sub_402E5D(&key, plain, &v3); 参数v3传出密钥
cpp
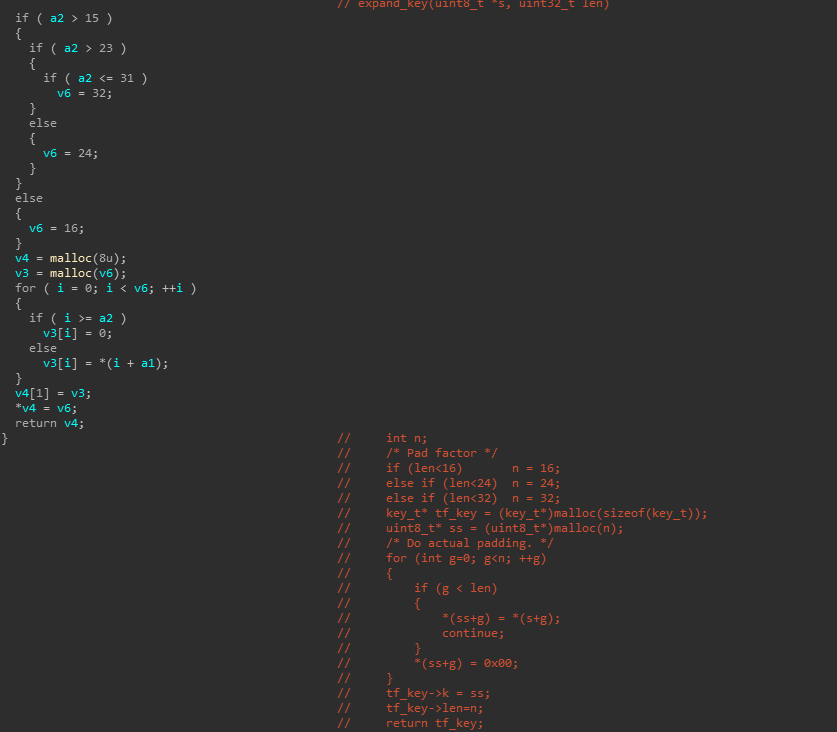
_BYTE *__cdecl sub_402E5D(int a1, int a2, int a3) |
下面来结合标准实现分析
cpp
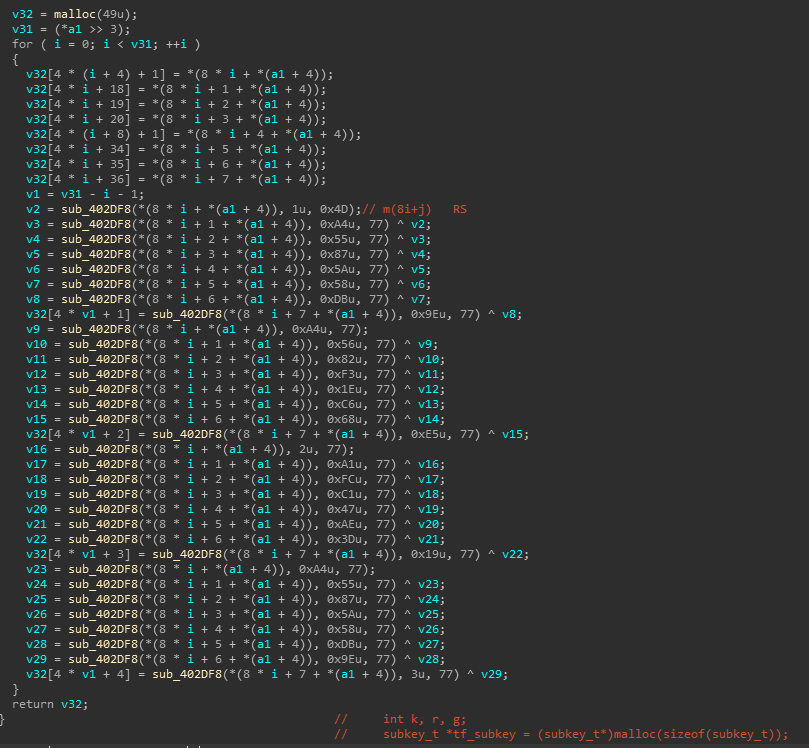
int __cdecl sub_401570(int a1, unsigned int a2) |
拓展密钥
可以看到题中对位数分析的判定进行了修改
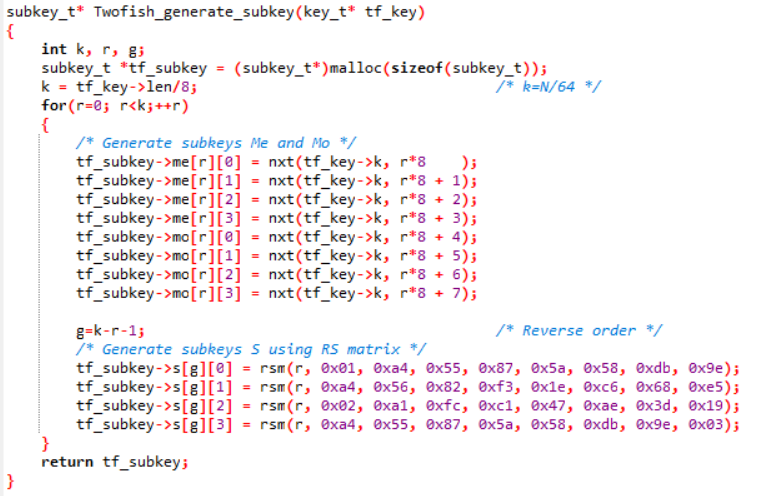
生成密钥
c实现
rsm函数定义为
cpp
|
k生成
h函数内部，可以看出，IDA将二维数组直接一维化
q0,q1都是256大小的数组
标准
cpp
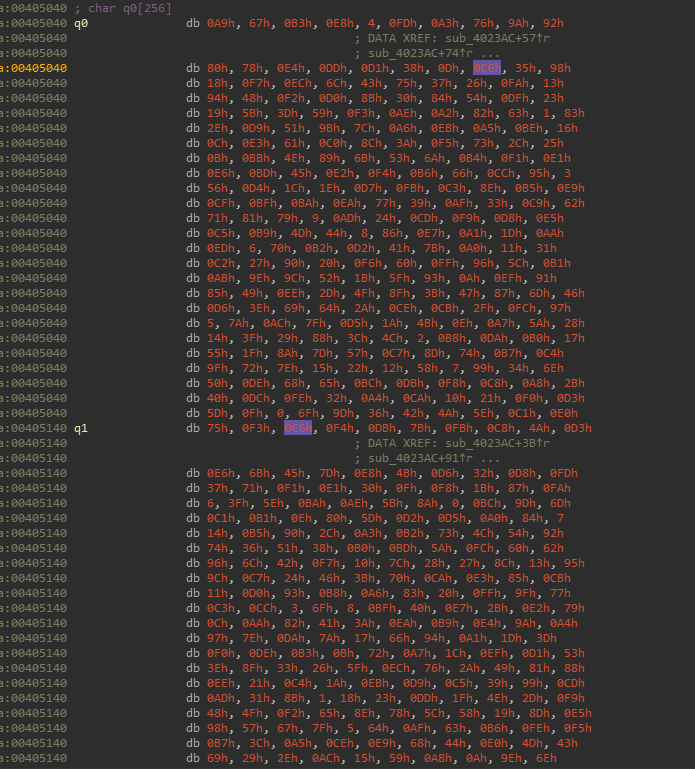
uint8_t q[2][256] = |
MDS矩阵运算
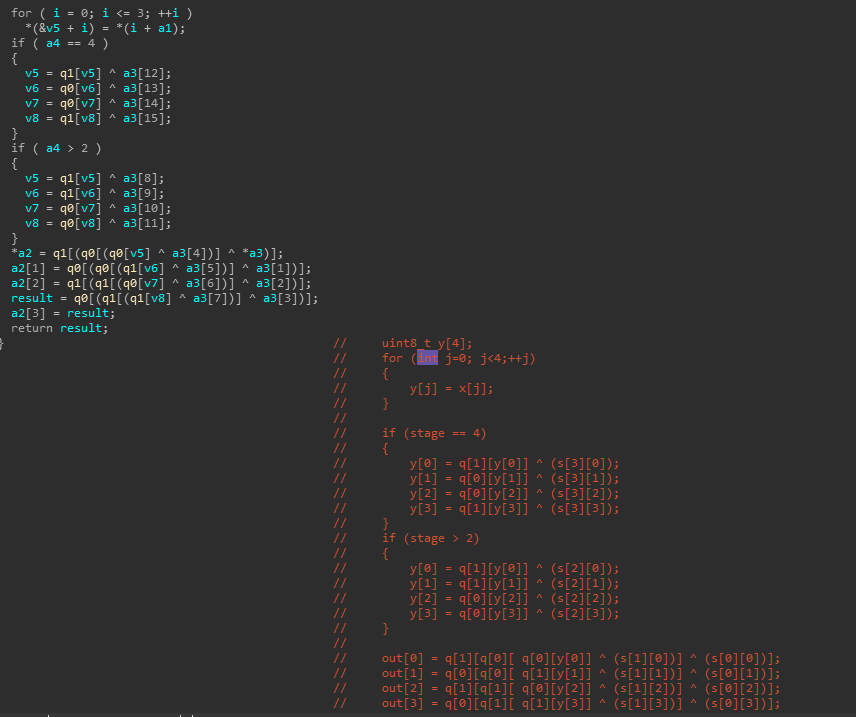
S-box生成
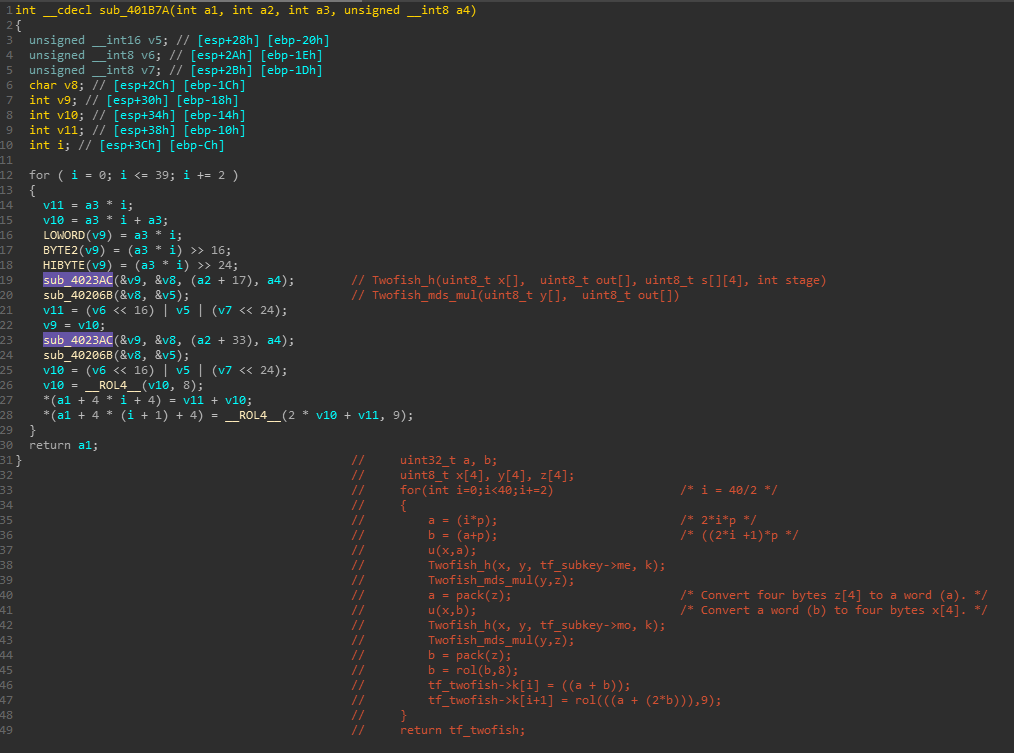
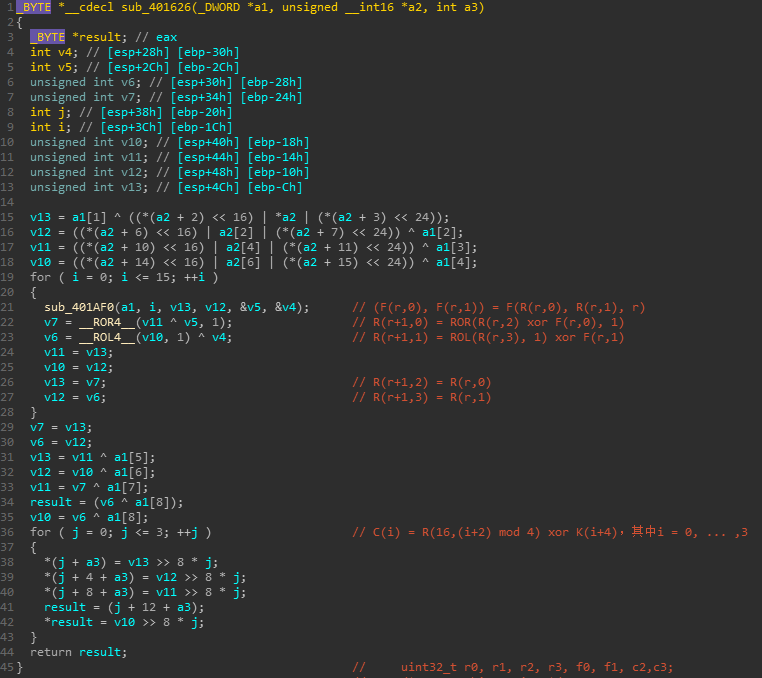
输入白化，循环，输出白化 sub_401626
c实现
f函数
算法解密
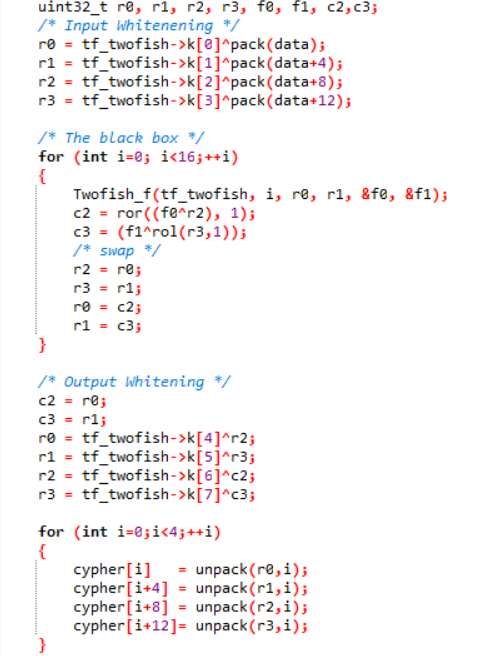
解密函数如下
cpp
void Twofish_decryt(twofish_t* tf_twofish, uint8_t *cypher, uint8_t *data) |
因此TwoFish加解密代码如下
twofish.h
cpp
|
tables.h
cpp
|
twofish.c
cpp
|
写一个main函数直接调用即可。
CTF出题变化分析
TwoFish算法共有三处可发生变化以提高出题难度
- rsm函数，0x14d可替换为其他数字
- Twofish_generate_ext_s_keys函数中gf的参数0x166可替换
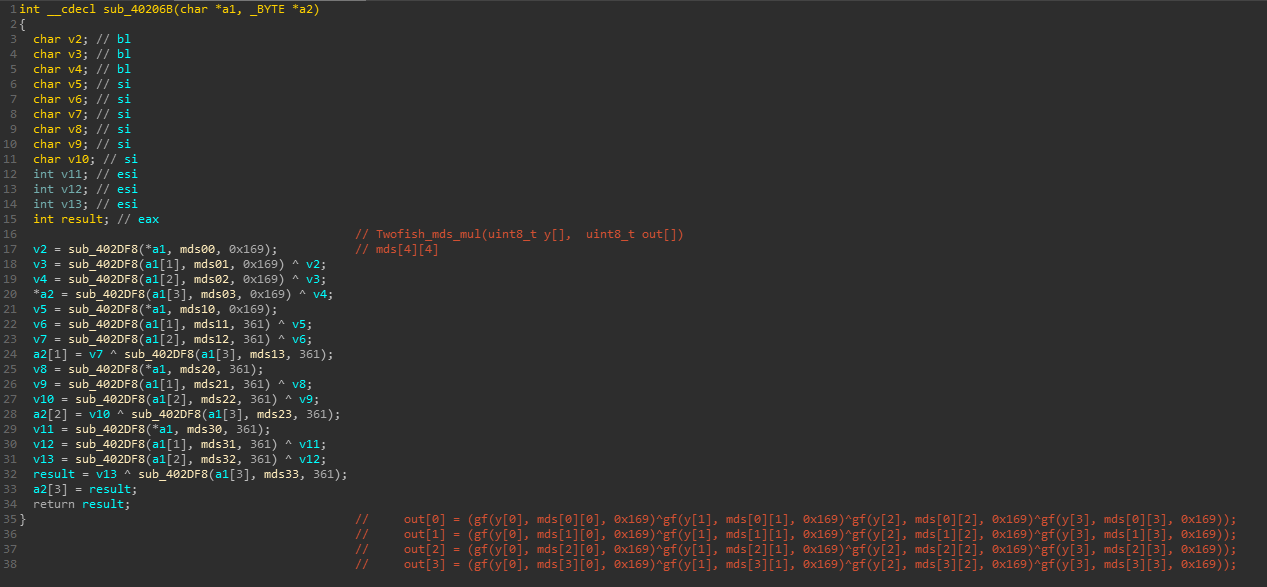
- Twofish_mds_mul函数中gf的参数0x166可替换
对于这类分组加密算法，即使插件没有识别，只要看出相关函数结构，就可以很快确定具体算法，找到可能变化的参数，相应修改解密函数即可
附件中附上了题目和idb文件供自行分析